Irányított gráfoknál az éleknek van irányuk. Ez azt jelenti, hogy ha például az 1-es csomópont össze van kötve a 2-vel, akkor fontos az él iránya is, hogy az 1-es vagy 2-es pont fele mutat. Ilyen esetben a szomszédossági mátrix nem feltétlen lesz szimetrikus a főátlóra nézve.

1. A következő nem irányított gráfnak hozzuk létre a szomszédossági mátrixát s írjuk ki a képernyőre.

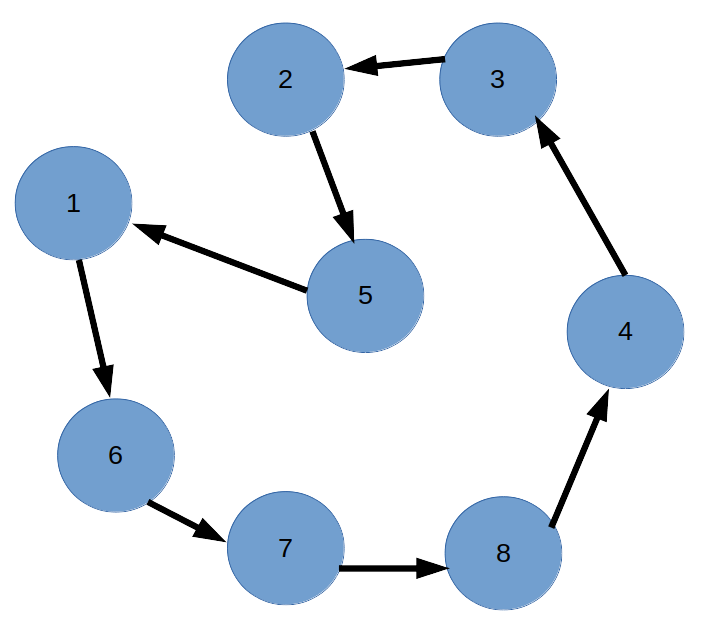
2. Írjunk egy programot, amely a fenti gráf egy tetszőleges csomópontjára kiírja, hogy annak van-e kapcsolata egy másik tetszőleges csomóponttal. Pl 2 5 re kiírja, hogy igen, 2 3 ra, hogy nem.

3. Írjunk egy programot, amely kiírja egy irányított gráf legtöbb kimenő éllel rendelkező csomópontját! Ha több ilyen van, a legkisebb indexűt írja ki!

4. Írjunk egy programot, amely kiírja egy irányított gráf legkevesebb bejövő éllel rendelkező csomópontját! Ha több ilyen van, a legkisebb indexűt írja ki!

5. Írjunk egy programot, amelyben létrehozunk egy irányított gráfot szomszédossági mátrixxal. A csúcsok számát s a szomszédossági mátrixot olvassuk be fileból.

Írjunk egy C++ programot, amely megvizsgálja, hogy lehetséges-e
úgy bejárni a gráfot, hogy miden élen csak egyszer haladunk át. (Vagyis hogy Euleri e a gráf).
Ha igen, kiírja, hogy a  graf euleri ha nem, kiírja, hogy a graf nem euleri.

6. Írjunk egy programot, amelyben létrehozunk egy gráfot szomszédossági mátrixxal. A csúcsok számát s a szomszédossági mátrixot olvassuk be fileból.
Aztán írjuk egy C++ programot, amely megvizsgálja, hogy lehetséges-e
úgy bejárni a gráfot, hogy miden csúcson csak egyszer haladunk át. (Vagyis hogy Hamiltoni e a gráf).
Ha igen, kiírja, hogy a graf hamiltoni, s kiír egy lehetséges utat új sorban.
Ha nem, kiírja, hogy a graf nem hamiltoni.